Goldener Schnitt
Um den Hintergrund des Goldenen Schnittes zu verstehen, müssen wir uns zuerst mit den Fibonacci Zahlen beschäftigen.
Leonardo Fibonacci hat das Wachstum der Kaninchenpopulation unter idealen Verhältnissen berechnet. Man kann feststellen dass diese Zahlenfolge sehr häufig in der Natur vorkommt (z.B. Blätter von Blumen, Spiralen der Tannenzapfen…) Die Zahlenfolge sieht wie folgt aus:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
Diese Folge ist auch bei der goldenen Spirale (Schnecken, Muscheln…) zu finden:
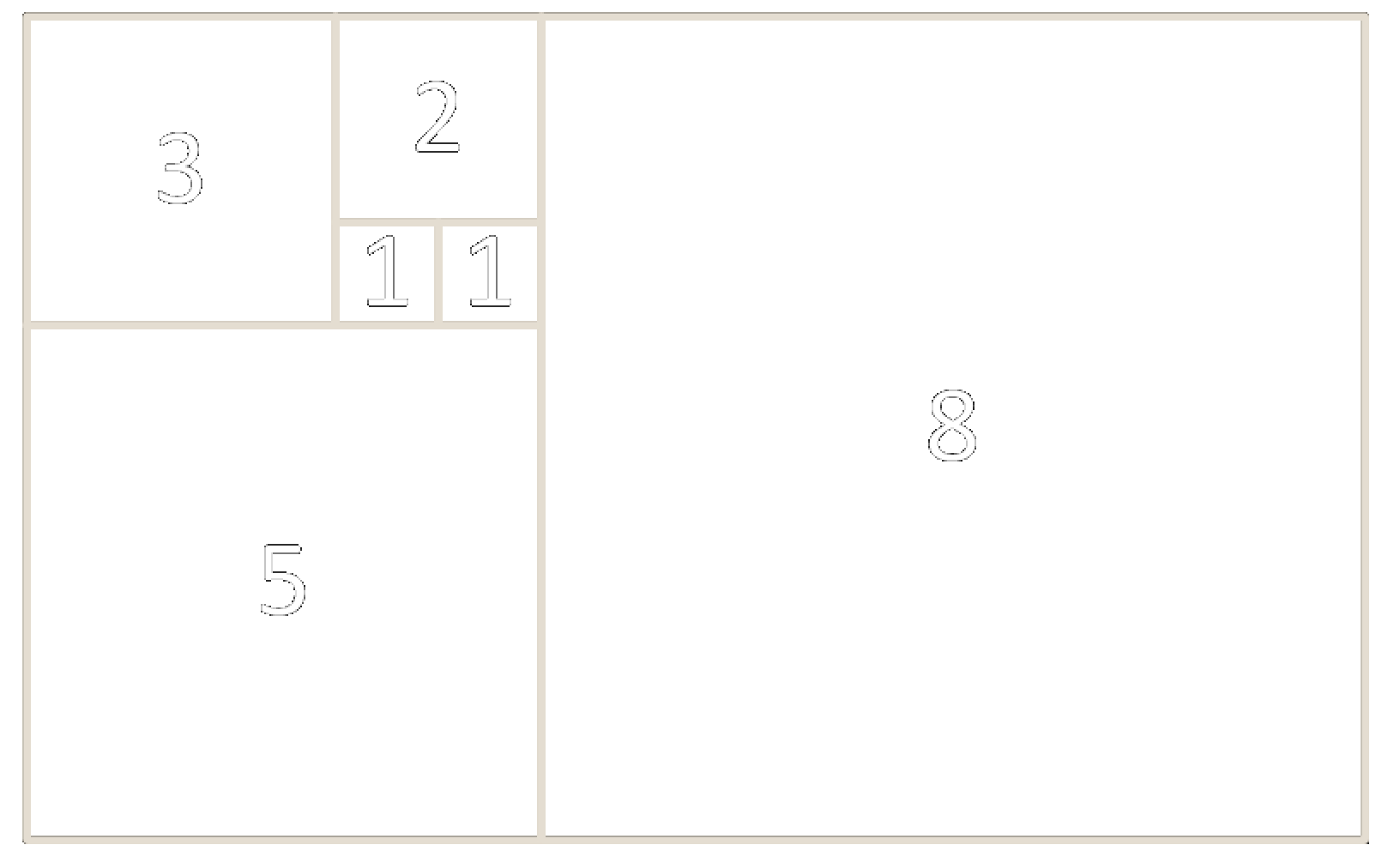
In diese Rechtecke wird nun die Spirale eingezeichent:
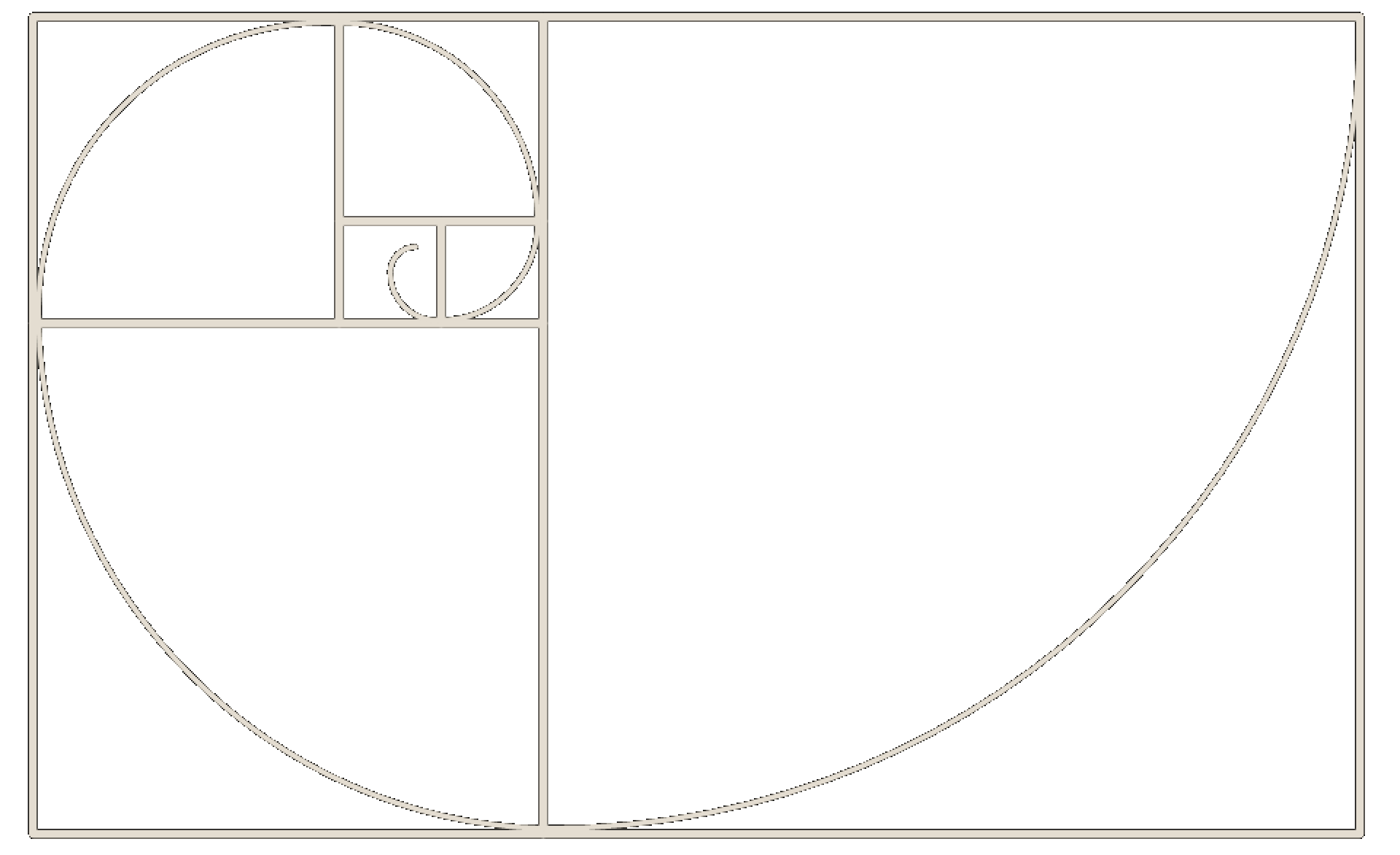
Das Ergebnis der Division mit der vorhergehenden Zahl nähert sich (je höher die Zahlen sind) dem goldenen Schnitt an (z.B. 89:55 = 1.6181818).
Nun kommen wir zum Goldenen Schnitt. Der Goldene Schnitt ist ein Verhältnis welches uns als sehr angenehm erscheint.
Als Goldenen Schnitt bezeichnet man das Teilungsverhältnis einer Strecke. Die Strecke teilt sich im Verhältnis von 61,8% zu 38,2% oder die grössere Strecke durch die kleinere im Faktor 1.618033988…
Dieses Verhältnis können wir sogar an unserem eigenen Körper beobachten (z.B. Verhältnis von Unterarm (mit Hand) zu Oberarm…).
Wenn wir nun unser Foto entsprechend aufteilen sieht das wie folgt aus:
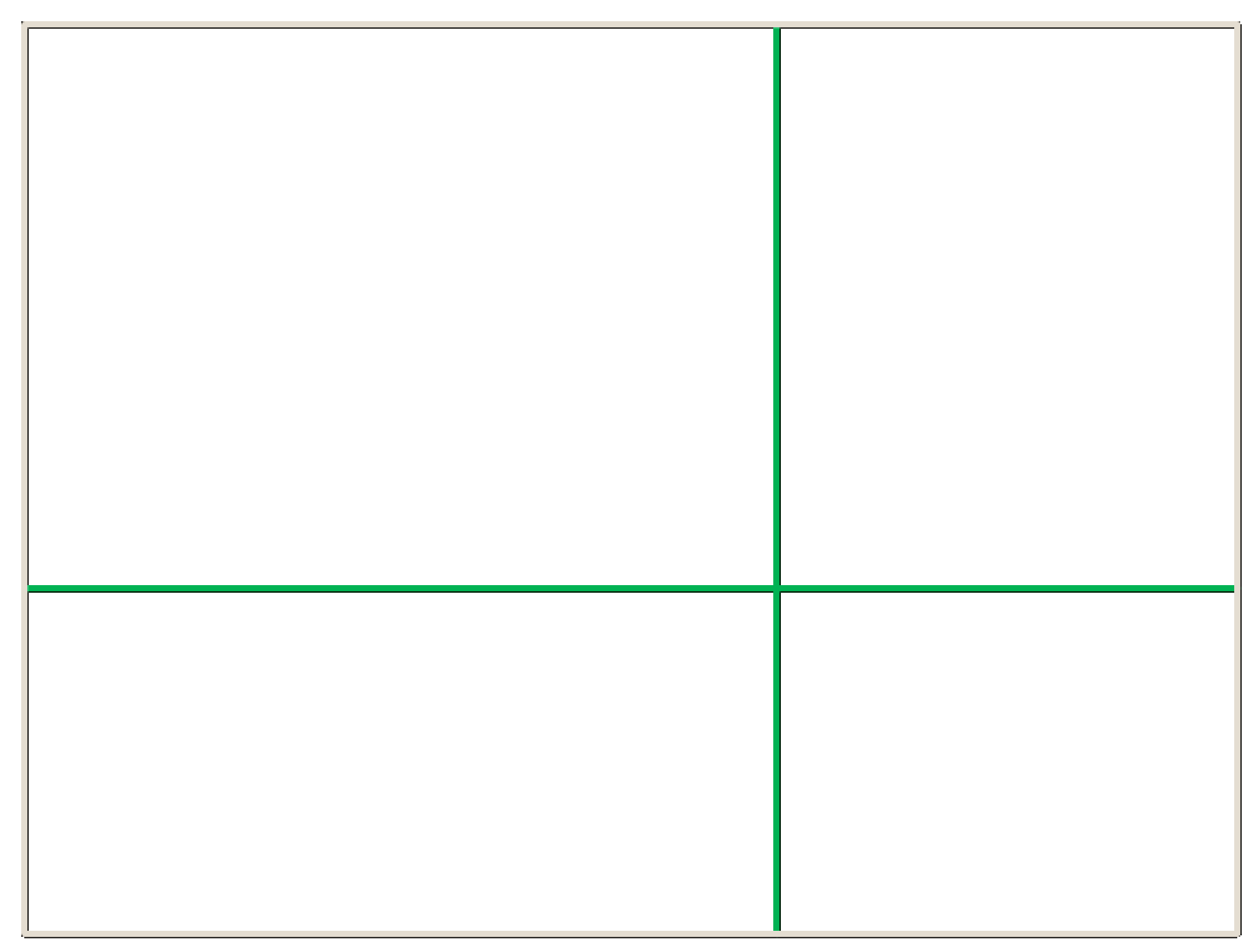
Da wir natürlich nicht immer dieses Verhältnis berechnen wollen, gibt es eine Annäherung die für uns besser vorstellbar ist:
Die 2:3 Regel. Das heisst wir teilen das Foto in 1/3 und 2/3 auf:
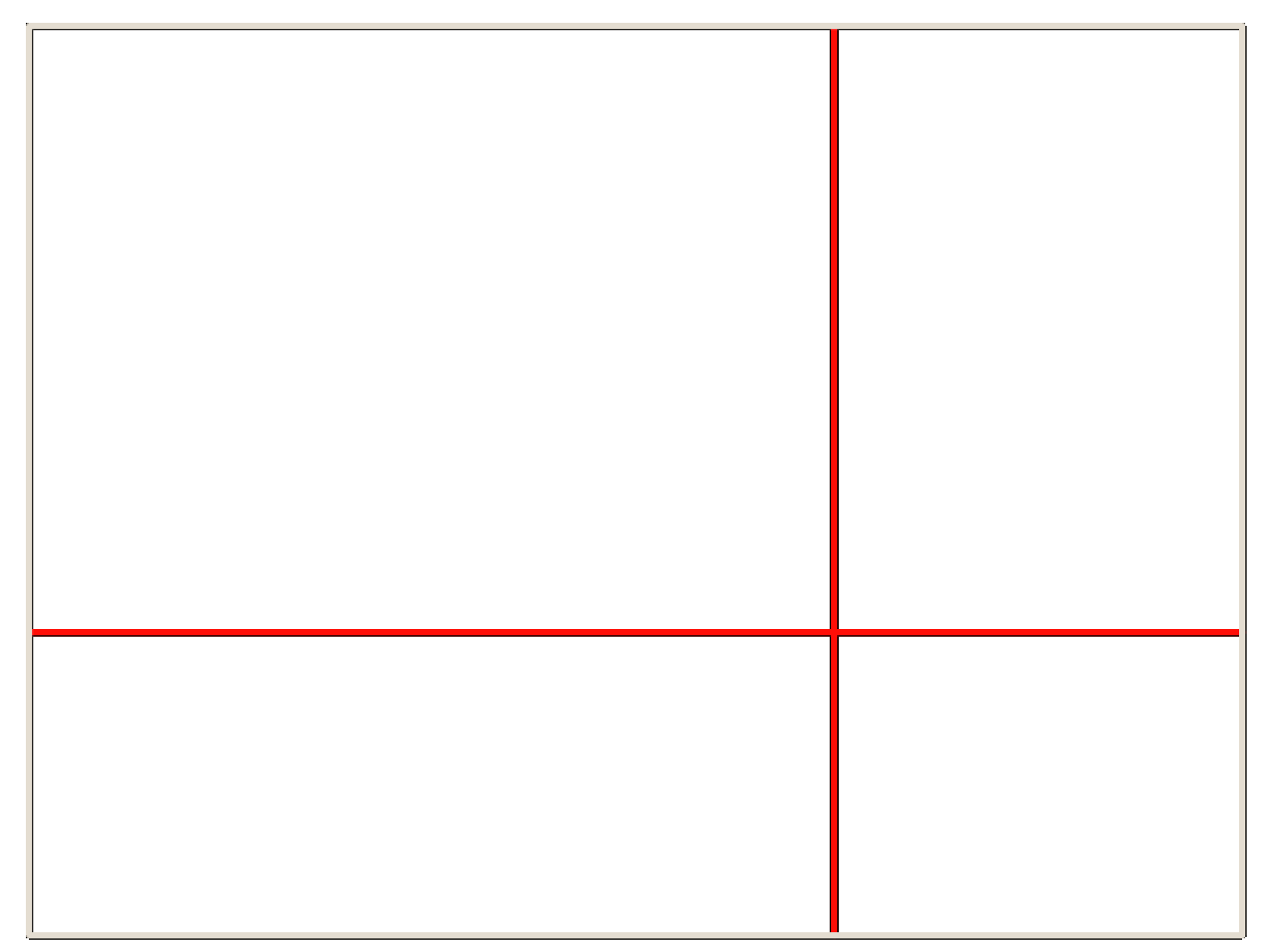
Wenn wir das nun zusammen vergleichen, gibt es keine grosse Abweichung zwischen den beiden Regeln:
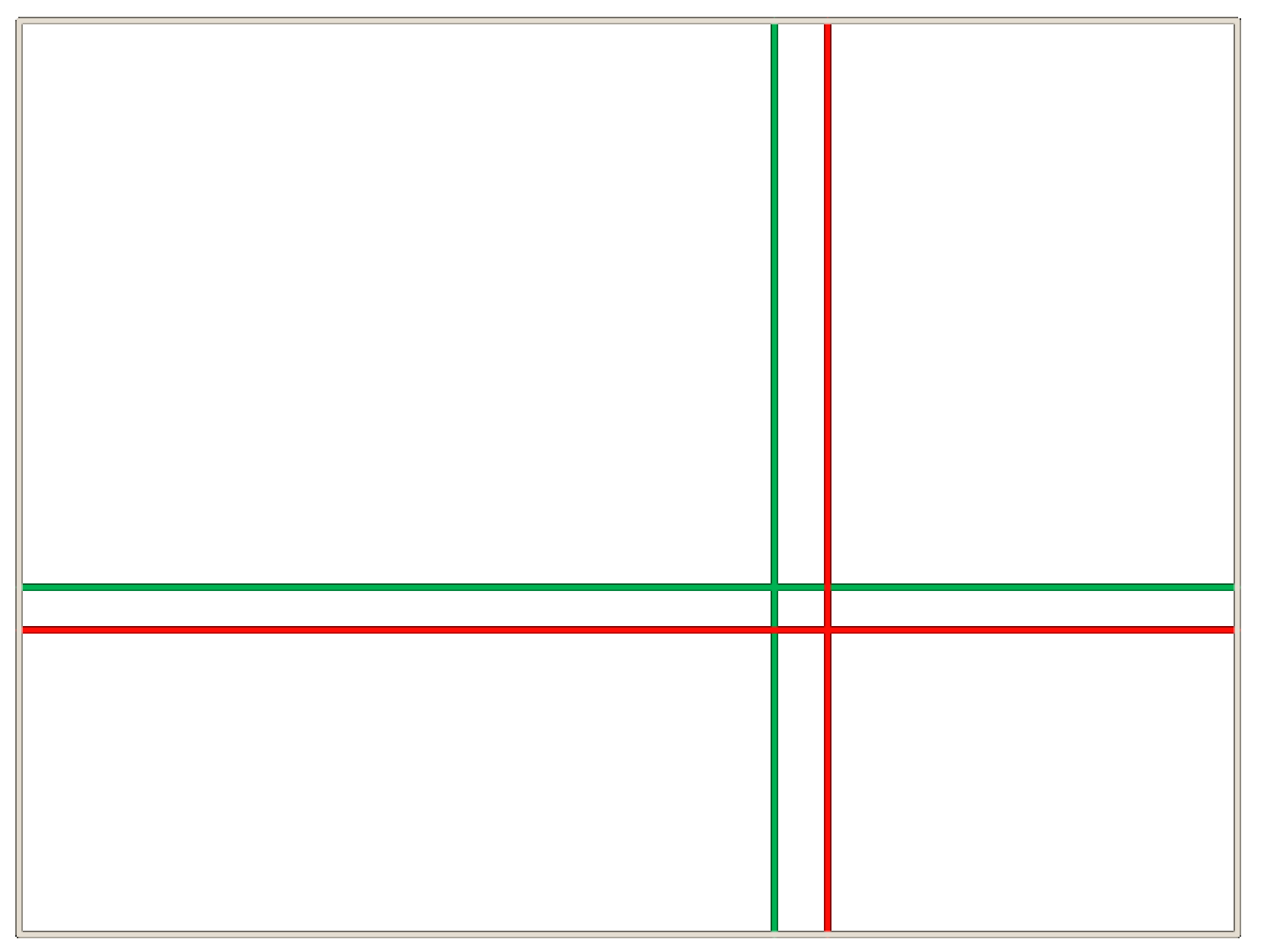
Wenn nun der Horizont oder das Motiv nicht mittig, sondern nach diesen Regeln platziert wird, wirkt das Bild für uns angenehmer und ausgewogener:

Weiter zu Histogramm
